カウンタ回路は数を数える回路です。ここでは2進数への理解を深めるという目的も兼ねてカウンタ回路の動きを紹介したいと思います。
この2進数というのは実はこれまでの説明の中でも度々使われています。2進数は「数」を表現するときの表現方法の1つです。私たちが普段「数」を表現するときに使っている方法は「10進数」という方法で、実はこの他にも「2進数」や「16進数」など様々な「数」の表現方法が存在します。
10進数というのは0から1つずつ数を足して行き、9に1を足した瞬間に「桁上がり」が発生することで初めて2桁の数である「10」になります。その後も各桁が9の次の数になる毎に桁上がりが発生するのが10進数のルールです。10進数では9の次の数で桁上がりが発生するので全ての「数」を0~9の数字だけで表現することができます。
それに対して2進数というのは0から1つずつ数を足して行くときに、1に1を足した瞬間に「桁上がり」が発生するルールで「数」を表現します。各桁が1の次の数、すなわち「2」になる毎に桁上がりが発生するのが2進数という数の表現方法になります。具体的に2進数の数を0から順に数えると次のようになります。
まずはスタートの数が「0」です。「0」の次の数は「1」です。「1」の次はもう桁上がりが発生してしまうので「10」です。その次は「11」です。「11」の次はまた1桁目で桁上がりが発生して、繰り上がった2桁目でも桁上がりが発生するので「100」になります。「100」の次は「101」です。
2進数で数を数えていくとすぐに桁が増えていってしまうので、人間が日常で使うにはとても不便な「数」の表現方法です。しかし2進数では全ての「数」を0と1の2種類の数字だけで表現することができます。この0と1だけで全ての「数」を表現できるという特徴は、全ての情報をONとOFFの組合せだけで表現するコンピュータの動作と非常に相性が良いのです。このような理由があるためにコンピュータ内での「数」の表現は全て2進数に合わせて作られています。
2進数での数の表現方法が分かったところで、実際に「数」を数えるカウンタ回路の動作について見ていくことにしましょう。
カウンタ回路も記憶回路の一種なのでフリップフロップ回路を組合せて作られています。まずはカウンタ回路の基礎となる回路を見てみましょう。下の図がその回路図になります。
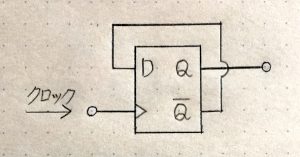
図60.カウンタ回路1
このフリップフロップ回路の特徴は反転出力端子(Qに上線がある記号の端子)の信号が入力端子Dへと戻されるような形で接続されていることです。反転出力が常に回路の入力となりますので、このフリップフロップ回路はクロック信号が入力される度に記憶している内容が0→1→0→1といった具合に、「0」と「1」が交互に入れ替わるような動作をします。
スポンサーリンク
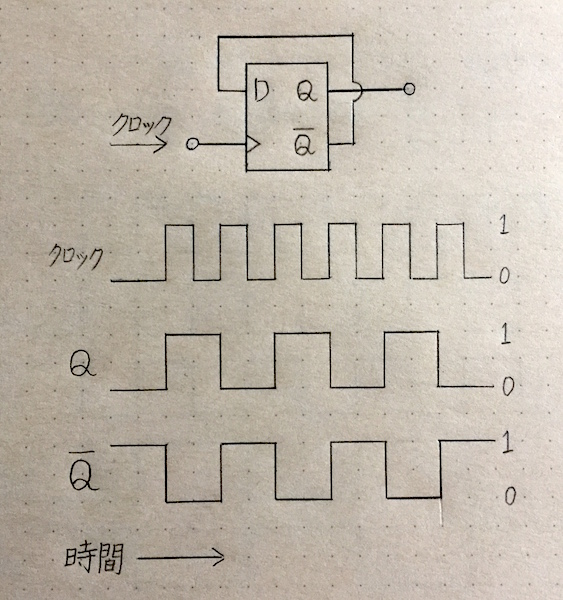
図61.カウンタ回路2
上図の信号波形で注目すべき点は出力端子Qの波形がクロック信号波形を時間方向に2倍分だけ引き延ばした波形になっていることです。
そこで上記のフリップフロップ回路と同じものをもう1つ用意して、2つ目の回路のクロック入力端子に1つ目の回路の反転出力端子(Q1に上線がある記号の端子)の信号をつなげてみます。
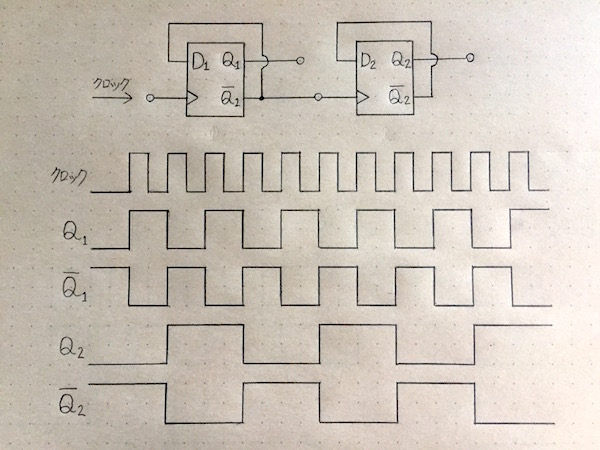
図62.カウンタ回路3
そうすると今度は2つ目の回路の出力端子Q2の波形が1つ目の回路の出力端子Q1の波形を時間方向に2倍分だけ引き延ばした波形になります。
同じ要領で3つ目、4つ目の回路を接続していくと後段の回路の出力が1つ前の回路の出力波形の2倍の長さになって出力されていきます。この回路の出力Qを図のように接続順に並べると、クロック信号を1つ入力する毎に2進数表示で数が1つずつカウントアップされていくカウンタ回路になっていることがわかります。
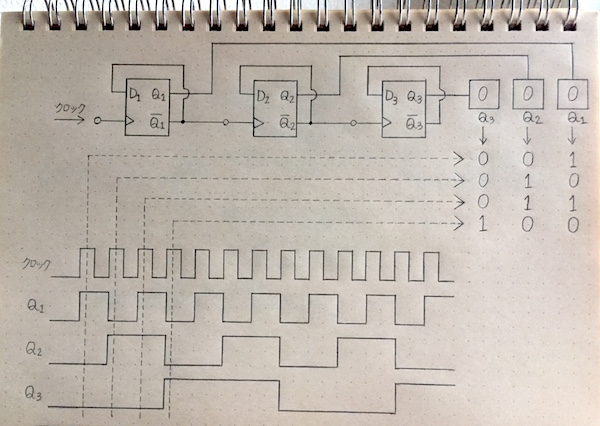
図63.カウンタ回路4
<戻る 次へ>




