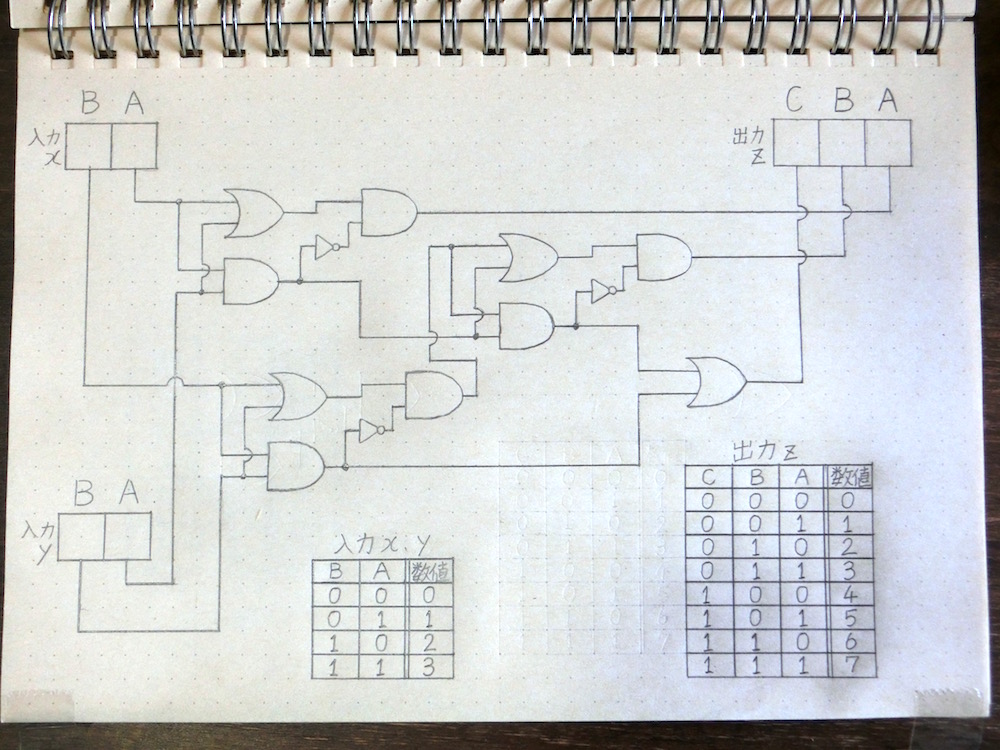
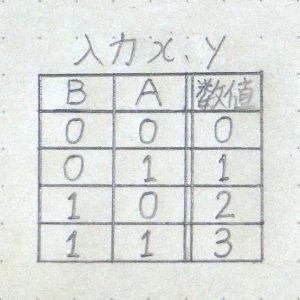
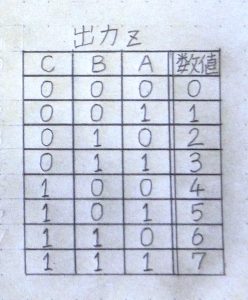
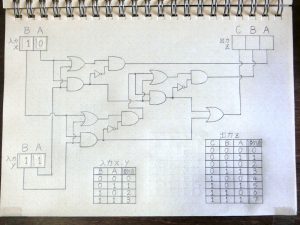
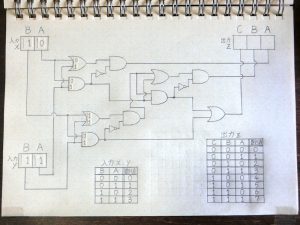
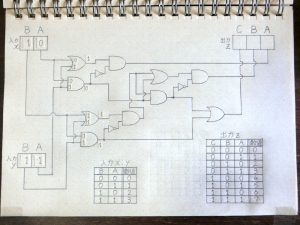
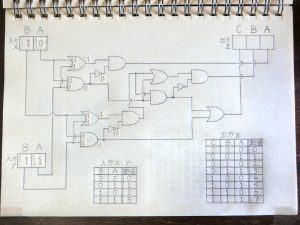
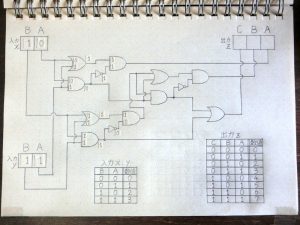
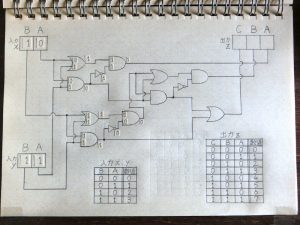
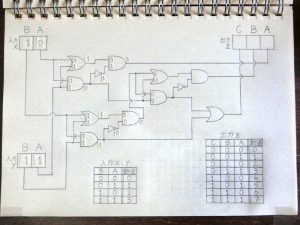
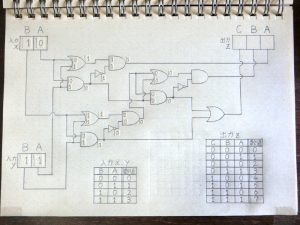
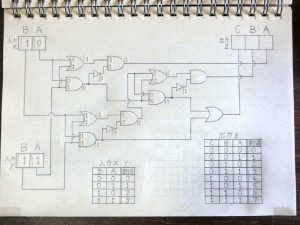
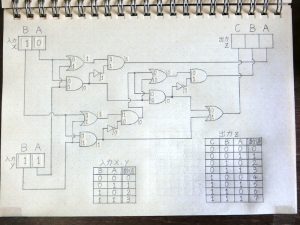
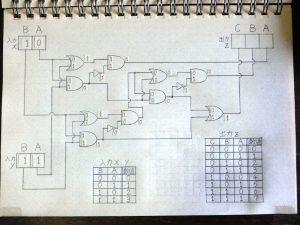
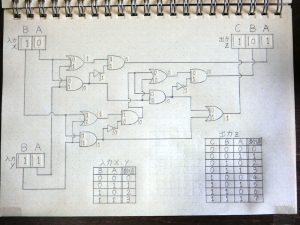
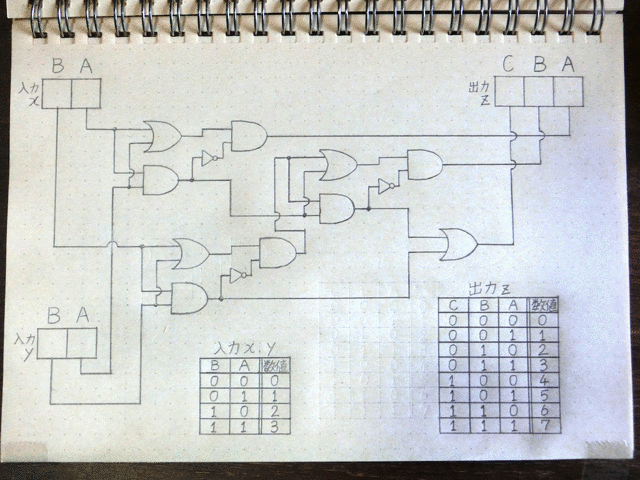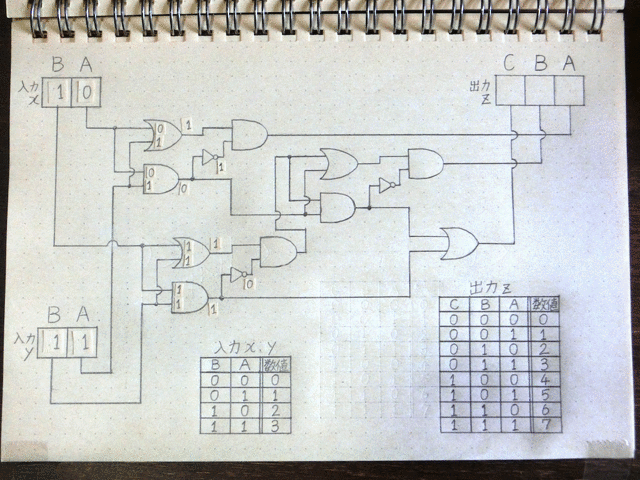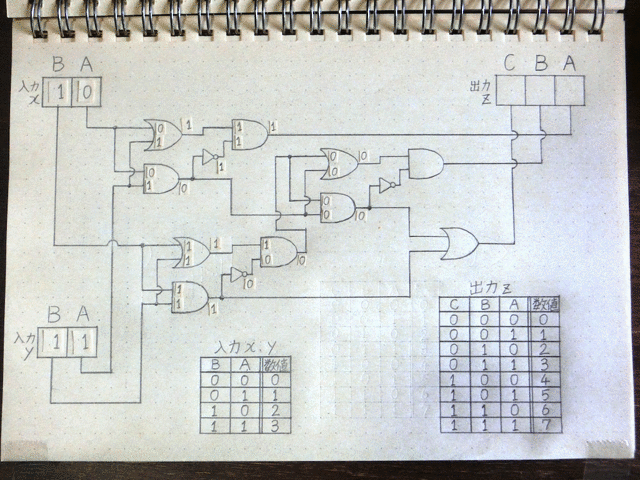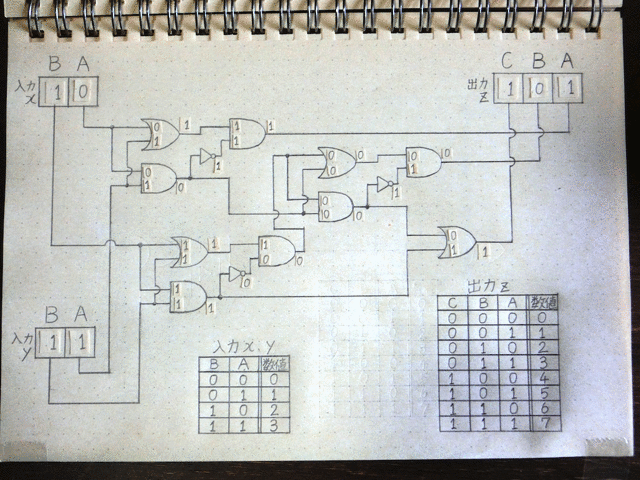
その後も前段の回路の出力が次につながる回路の入力へと伝わる形で信号の加工処理が進んでいきます。
図23.加算回路5
図24.加算回路6
図25.加算回路7
図26.加算回路8
図27.加算回路9
図28.加算回路10
図29.加算回路11
図30.加算回路12
最終的に出力zのC端子には1、B端子には0、A端子には1が出力されました。出力数値のパターン表からこの結果は数値の「5」を表していることが分かります。
最初に入力xと入力yに入力した数値は「2」と「3」ですので、2+3=5という足し算の結果が電気的な仕組みによって自動的に計算されたことがわかると思います。はじめは不思議に思えるかもしれませんが入力する数値を他の数値に変えてみてもちゃんと結果は入力x+入力yの答えが出てくるようになっています。いろいろな数値を入力して実験してみてください。
図31.加算回路の動作
ここまで来ると少しコンピュータの中身についてイメージが湧いてきたのではないでしょうか。トランジスタという単純なスイッチ機能しか持たない部品でも、うまく組合せることで計算機能を実現することができます。最終的にコンピュータを完成させるためにはこの他にもいくつかの機能が必要になってきますが、それらの機能も全てトランジスタという単純なスイッチ動作の組合せでできています。
上で示した足し算回路は実験用に回路規模を小さくしてありますが、もちろん回路規模を大きくして入出力端子を増やすこともできます。実際に用いられているコンピュータでは小さいものでも数値を8つ以上の端子で扱うことが多いです。例えば入出力ともに8つの端子を持つ足し算回路を作る場合は、端子H、端子G、端子F、端子E、端子D、端子C、端子B、端子Aという具合に、入力x、入力y、出力zそれぞれに8つの端子を持つことになります。8つの「1」と「0」の組合せで数値を表現できるので0~255までの、256通りの数値を扱える足し算回路になります。(ちなみにここで言うような端子の数のことを「ビット」と呼びます。8つの端子で計算を行うコンピュータのことは8ビットコンピュータなどと呼ばれます。)
0~255までの数値を使った足し算となると組合せの数が膨大になりますので、回路規模が大きくなっても正しく計算ができるのか不安かもしれませんが、ちゃんとできるようになっています。同じような仕組みで引き算回路も作ることができます。そしてデジタル回路で作れるのは計算回路だけではありません。どのような入力があった時に出力端子にどのパターンを出力すべきかがはっきりと決まっているものであれば、そのルールに従って動作する回路を全て「NOT回路」「OR回路」「AND回路」の組合せだけで作れるようになっているのです。
例えば入力端子に複数のセンサーの出力を接続し、出力端子に複数の電球やモーターを接続しておいて「どのセンサーがONになった時にどの電球とモーターをONにするか」といった具合に入力パターンと出力パターンの対応さえ決めることができれば、そのようなルールで動作するような回路も「NOT回路」「OR回路」「AND回路」の組合せで作ることができます。
実際の回路の作り方としては「カルノー図法」というものがあるのですが、今では入力パターンと出力パターンの対応さえ決めてしまえばあとは専用のソフトウェアが自動で回路を出力してくれますので、自分でこの問題を解く機会はほとんどないと思います。ですのでここではコンピュータの仕組みをイメージするためにデジタル回路で計算を行うことができるということを説明するだけにとどめておこうと思います。