まず、hieを以下の式で近似して求める方法です。（入力インピーダンス「hie」という表現ではなく入力抵抗「ri」という表現のときもあります。）

入力インピーダンス hie = 0.026 × hFE / コレクタ電流 IC

比較的に求めやすいhFEと熱電圧（26mV）という定数を使った近似式です。コレクタ電流は大抵の場合に[mA]で表すぐらいの大きさで設計されるので、あらかじめ単位が[mA]で表したときの数値をそのまま代入できるようにした以下の形の式で載っていることもありました。

入力インピーダンス hie = 26 × hFE / コレクタ電流 IC [mA]

　　※この式はコレクタ電流が[mA]で表されることを前提に、あらかじめ式に×1000されている。例えばコレクタ電流が2mAの時は”2”をそのままICに代入して計算する。

あと、本によっては以下のような近似式も見られました。（この式もコレクタ電流は[mA]で表されることを前提に、あらかじめ式に×1000されている。）

入力抵抗 ri = 30 × hFE / コレクタ電流 IC [mA]

 

相互コンダクタンスを用いた電圧増幅度の計算

この他にも、「相互コンダクタンス」を使って電圧増幅度を求める式もあります。

電圧増幅度 Av = 相互コンダクタンス gm × 負荷抵抗 RL

　　　　　　　= ( コレクタ電流 IC / 熱電圧 VT ) × 負荷抵抗 RL

　　　　　　　= コレクタ電流 IC × 負荷抵抗 RL / 26mV

VT：熱電圧≒( 26mV )

熱電圧 VT = k × T / q ≒ 26mV

k：ボルツマン定数 1.3806488×10－23

T：絶対温度 300[K]

q：電子電荷 1.602177×10－19

この式も一見違う式に見えますが、熱電圧≒26mVという近似式を使って電圧増幅度を求めているという意味で上の式と同じ内容になります。

相互コンダクタンスというのは「ベース・エミッタ間電圧を変化させた時にどれだけコレクタ電流が変化するか」を示した、ベース・エミッタ間電圧とコレクタ電流の比を表す数値です。（単位は[S]で、ジーメンスと読みます。）

相互コンダクタンスの定義を見てもわかるとおり、この数値に負荷抵抗の数値をかけるだけで簡単に電圧増幅度になります。相互コンダクタンスと熱電圧との以下の関係式を覚えておくと一気に電圧増幅度の計算が簡単になります。

相互コンダクタンス gm = コレクタ電流 IC / 熱電圧 VT( 26mV )

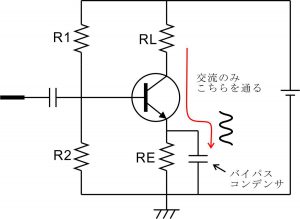
電流帰還バイアス回路（エミッタ抵抗の一部にバイパスコンデンサを入れる方式）の電圧増幅度

また、電流帰還バイアス回路でエミッタ抵抗にバイパスコンデンサを入れる際、エミッタ抵抗全てをバイパスするのではなく、一部分だけ残すやり方もあります。この場合は交流的に見て残った分のエミッタ抵抗値を使って電圧増幅度を計算します。

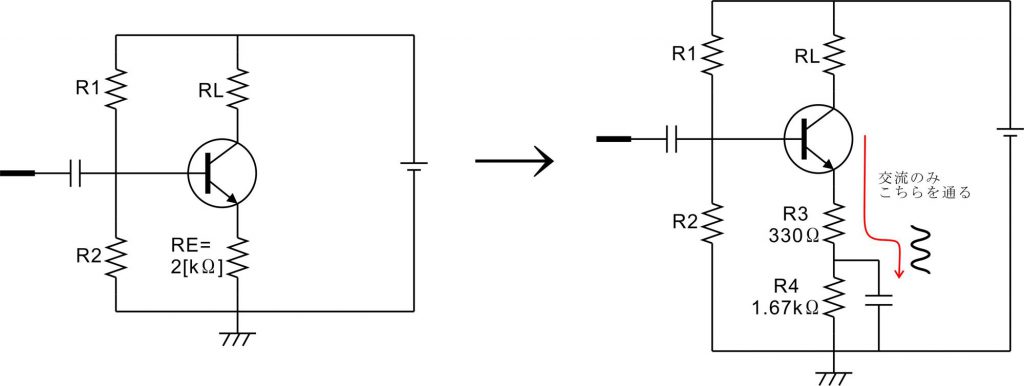
まずはエミッタ抵抗を２つに分割してその片方にだけバイパスコンデンサを入れるやり方です。以下の回路では交流的に見ても分割した330Ω分だけはエミッタ抵抗値として残るので、電圧増幅度の式は330Ωのエミッタ抵抗を持った回路として計算します。

電圧増幅度 Av = 負荷抵抗 RL / 抵抗 R3

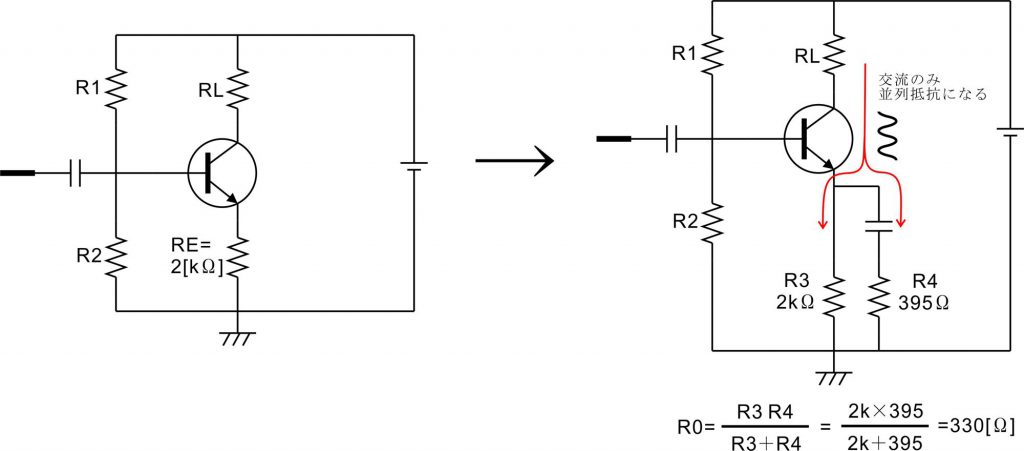
次の回路は2kΩのエミッタ抵抗をわざわざ分割したりせず、隣に並列に回路を追加することによって全体の抵抗値を低く見せるというやり方です。この回路は直流的に見ればエミッタ抵抗は2kΩのままなのですが、交流的に見れば抵抗R3とR4が並列に接続されたことになりますので、その合成抵抗分の値がエミッタ抵抗値になるものとして電圧増幅度を計算します。

電圧増幅度 Av = 負荷抵抗 RL / 合成抵抗 R0