電流帰還バイアス回路ではエミッタ抵抗と負荷抵抗の比で簡単に電圧増幅度の計算ができました。(詳しくはこちらのページをご覧ください。)
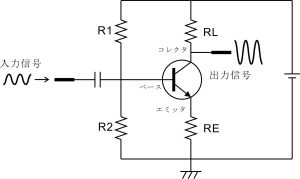
電圧増幅度 vout / vin = 負荷抵抗 RL / 抵抗 RE
しかし、上の回路図ではエミッタ抵抗REでの電圧降下分だけ出力端子が上下できる電圧範囲が減ってしまいます。そこでエミッタ抵抗REに並列になるようにコンデンサを入れて、交流的に見た時に抵抗REが無かったように見せるというテクニックが良く使われます。このような目的で使用されるコンデンサのことをバイパスコンデンサと言います。コンデンサは交流信号は素通りさせて直流信号は遮断する特性があるので、バイパスコンデンサを入れても直流で動作しているバイアス回路の設計に影響を与えることはありません。
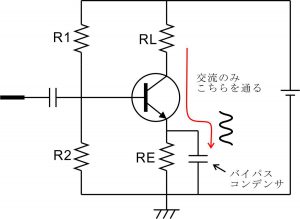
エミッタ抵抗にバイパスコンデンサを接続すると、交流信号は抵抗REよりもバイパスされたコンデンサの方を通るようになります。(交流にとってコンデンサは抵抗0の配線のように見える。)こうなると交流的に見たときのエミッタ抵抗は非常に低くなりますので、電圧増幅度の分母が小さくなり、電圧増幅度が増すことになります。
電圧増幅度 vout / vin = 負荷抵抗 RL / 抵抗 RE ← 分母が非常に小さくなる。
エミッタ抵抗が0になってしまうと上記の式では電圧増幅度が無限大になってしまうので、エミッタ抵抗にバイパスコンデンサが付いている場合は電流帰還バイアス回路であっても固定バイアス回路や自己バイアス回路と同じように以下の式を使って電圧増幅度を計算します。
電圧増幅度 Av = hFE × RL / hie
RL:負荷抵抗
hie:トランジスタの入力インピーダンス(入力抵抗)
ただ、この電圧増幅度の式にはhieという求めにくいパラメータが使われています。実際に電圧増幅度を求めたい場合は以下の近似式を使った方が便利です。
電圧増幅度 Av = 相互コンダクタンス gm × 負荷抵抗 RL
スポンサーリンク
= ( コレクタ電流 IC / 熱電圧 VT ) × 負荷抵抗 RL
= コレクタ電流 IC × 負荷抵抗 RL / 26mV
VT:熱電圧≒( 26mV )
熱電圧 VT = k × T / q ≒ 26mV
k:ボルツマン定数 1.3806488×10-23
T:絶対温度 300[K]
q:電子電荷 1.602177×10-19
電圧増幅度に関して、詳しくはこちらのページをご覧ください。
また、電流帰還バイアス回路でエミッタ抵抗にバイパスコンデンサを入れる際、エミッタ抵抗全てをバイパスするのではなく、一部分だけ残すやり方もあります。この場合は交流的に見て残った分のエミッタ抵抗値を使って電圧増幅度を計算します。
まずはエミッタ抵抗を2つに分割してその片方にだけバイパスコンデンサを入れるやり方です。以下の回路では交流的に見ても分割した330Ω分だけはエミッタ抵抗値として残るので、電圧増幅度の式は330Ωのエミッタ抵抗を持った回路として計算します。
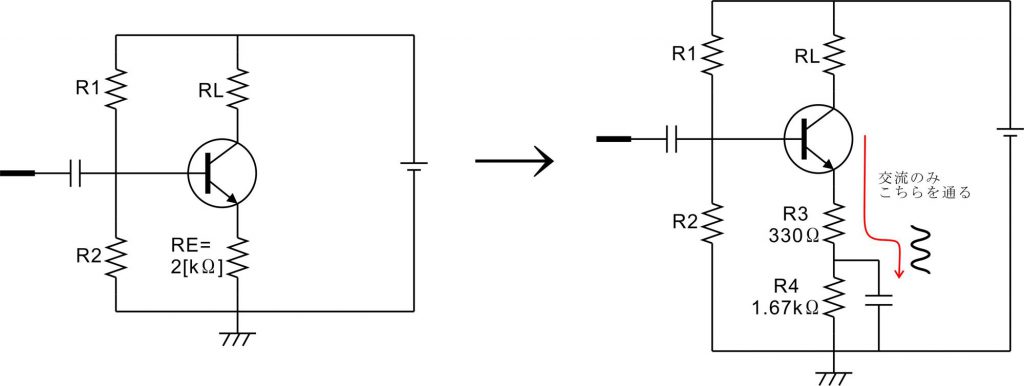
電圧増幅度 Av = 負荷抵抗 RL / 抵抗 R3
次の回路は2kΩのエミッタ抵抗をわざわざ分割したりせず、隣に並列に回路を追加することによって全体の抵抗値を低く見せるというやり方です。この回路は直流的に見ればエミッタ抵抗は2kΩのままなのですが、交流的に見れば抵抗R3とR4が並列に接続されたことになりますので、その合成抵抗分の値がエミッタ抵抗値になるものとして電圧増幅度を計算します。
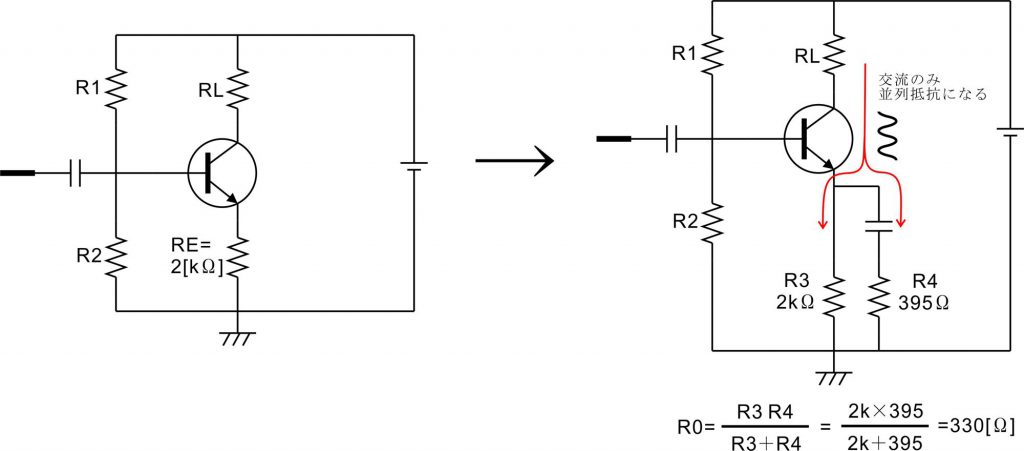
電圧増幅度 Av = 負荷抵抗 RL / 合成抵抗 R0




