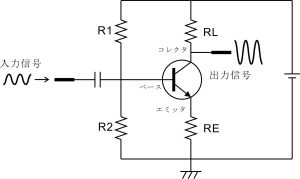
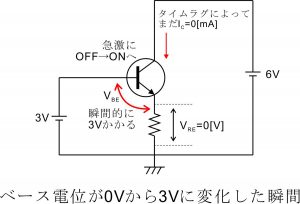
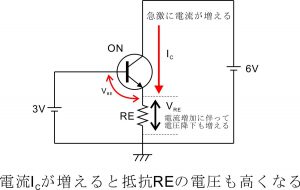
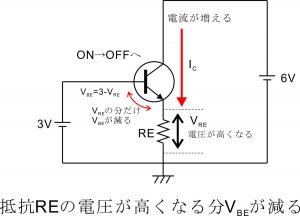
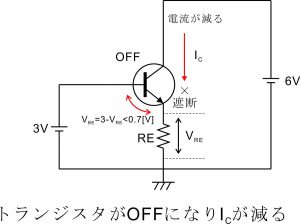
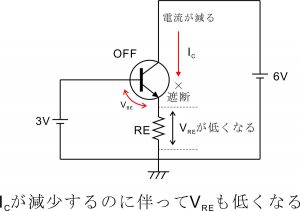
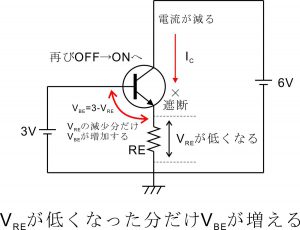
上記の思考実験からも分かる通り、トランジスタのベース・エミッタ間電圧は常に0.7V付近に維持されるようになっています。この状態でベースに微小な信号波形を入力するとベース電位がわずかに上下するその動きに連動して抵抗REの電圧VREも上下します。(なぜならベース・エミッタ間電圧は常に0.7Vに維持され、ベース電位 = ベース・エミッタ間電圧0.7V + 抵抗REの電圧降下VRE であるから。)
抵抗REの電圧が入力信号vin分だけ上下するとコレクタ電流ICの変化量は以下のようになります。
コレクタ電流の変化量 = 入力信号vin / 抵抗RE
コレクタ電流が変動するとその動きに連動して負荷抵抗RLでの電圧降下も大きくなったり小さくなったりします。負荷抵抗RLの直下に設定された出力端子の電位変化量voutは以下のように表すことができます。
出力端子の電位変化量 vout = 負荷抵抗 RL × コレクタ電流の変化量
= 負荷抵抗 RL × 入力信号 vin / 抵抗 RE
上記の式より電圧増幅度( vout / vin )を以下のように表せることが分かります。
電圧増幅度 vout / vin = 負荷抵抗 RL / 抵抗 RE
上記の式にもhFEは出てきません。電流帰還バイアス回路はバイアス電圧の設計だけでなく電圧増幅度の設計にもhFEを使わずに済むので大変便利な回路です。
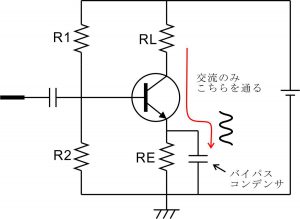
ですが抵抗REで電圧降下が発生するとその分出力電位を上下させられる範囲が狭まってしまうので、抵抗REに並列になるようにコンデンサを入れて、交流的に見た時に抵抗REが無かったように見せるというテクニックが良く使われます。このコンデンサのことをバイパスコンデンサと言います。コンデンサは交流信号は素通りさせて直流信号は遮断する特性があるので、バイパスコンデンサを入れても直流で動作しているバイアス回路の設計に影響を与えることはありません。(バイパスコンデンサについて詳しくはこちらのページをご覧ください。)
バイパスコンデンサを抵抗REに入れると交流的には抵抗REが無かったことになるので上記の電圧増幅度の式は使えなくなってしまいます。この場合の電圧増幅度の式は以下のようになります。
電圧増幅度 Av = hFE × RL / hie
RL:負荷抵抗
hie:トランジスタの入力インピーダンス(入力抵抗)
ただ、この電圧増幅度の式にはhieという求めにくいパラメータが使われています。実際に電圧増幅度を求めたい場合は以下の近似式を使った方が便利です。
電圧増幅度 Av = 相互コンダクタンス gm × 負荷抵抗 RL
= ( コレクタ電流 IC / 熱電圧 VT ) × 負荷抵抗 RL
= コレクタ電流 IC × 負荷抵抗 RL / 26mV
VT:熱電圧≒( 26mV )
熱電圧 VT = k × T / q ≒ 26mV
k:ボルツマン定数 1.3806488×10-23
T:絶対温度 300[K]
q:電子電荷 1.602177×10-19
電圧増幅度に関して、詳しくはこちらのページをご覧ください。
電流帰還バイアス回路の具体例
最後に電流帰還バイアス回路を使った具体的な回路を見て行きます。ここでは使用するトランジスタのhFEを200、回路の電源電圧を12Vとし、電圧増幅度が5倍になるような増幅器を設計するものとします。
まず、適当な値としてコレクタ電流ICは2mA流すことにします。
コレクタ電流ICの値が決まったら、不可抵抗RLを、IC × RL が、だいたい電源電圧の半分ぐらいになるように決めます。(RLに現れる増幅後の出力波形が、上下に振幅する余裕を確保するために、無入力時のIC × RL は電源電圧の真ん中ぐらいに設定します。このことを「動作点」を決める。と言います。)今回はREでの電圧降下も必要なので、真ん中よりやや上の方に設定します。
IC × RLが5Vになるように決めます。コレクタ電流ICは2mAなので、負荷抵抗RLは5V / IC=2.5kΩになります。
次にエミッタ抵抗REを決めます。今回設計する増幅回路は5倍の電圧増幅度を持たせるため、抵抗RLが決まると同時に負荷抵抗REの値も決まります。電流帰還バイアス回路の電圧増幅度は以下の式で表されるため
電圧増幅度 Av = 負荷抵抗 RL / 抵抗 RE
5倍の増幅度にする場合はREの値を、Av = 負荷抵抗 RL / 抵抗 RE = 5 となるように設定します。
RE =負荷抵抗RL / 5 となり、負荷抵抗RLは2.5kΩなので、RE = 500Ω となります。
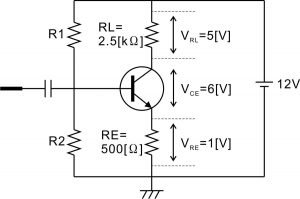
RLが2.5kΩ、REが500Ωであるとすると、入力に何も信号が入っていない状態でのトランジスタの出力側は以下のようになっています。
上の図でまず確認することはコレクタ損失PCが最大定格以下に収まっているかどうかです。コレクタ損失とはコレクタ・エミッタ間で熱となって失われていく電力損失のことで、コレクタ端子とエミッタ端子の間の電位差VCEにコレクタ電流をかけた値で計算することができます。
コレクタ・エミッタ間の電位差 VCE = 電源電圧 – RLの電圧降下 – REの電圧降下
= 12V – (2.5kΩ × 2mA) – (500 × 2mA) = 6[V]
コレクタ損失 PC = コレクタ・エミッタ間の電位差 VCE × コレクタ電流IC
= 6V × 2mA = 12[mW]
コレクタ損失の最大定格はトランジスタのデータシートなどで確認します。
次に出力端子の最大振幅についても確認します。この回路の場合、出力端子は電源電圧から-5Vの電位を中心に振動することになります。なので上側には5Vまで、下側にはコレクタ・エミッタ間の電位差VCE(6V)分だけ振れる余裕があります。(厳密にはコレクタ・エミッタ間飽和電圧が確保できている必要があります。)
次にベース電位を決定するために抵抗R1とR2について見て行きます。抵抗REでの電圧降下は500Ω × 2mA = 1V でしたので、ベース電位は1V + 立上り電圧0.7Vで1.7Vにすれば良いことがわかります。抵抗R1とR2の抵抗分圧でこの1.7Vを作れば良いことがわかりましたが、ベースへ流れ込む電流を十分小さな値として無視できるように、抵抗R1とR2に流れる電流はベース電流から見て十分大きな電流にする必要があります。
コレクタ電流は2mAであると先ほど決定しました。使用するトランジスタのhFEが200ですので、ベースに流れる電流IBはIB = 2mA / 200の、0.01mAということになります。IBに対して大体10倍以上あれば十分大きな電流であると考えられますので、抵抗R1とR2に流れる電流を0.01mA × 10で、0.1mA流すことにします。
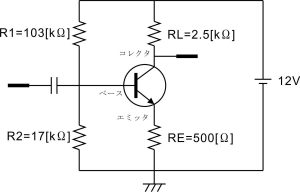
電源電圧の12VをR1とR2の抵抗分圧でそれぞれ10.3Vと1.7Vにすれば良いのでR1とR2はそれぞれ以下の抵抗値とすれば良いことがわかります。
R1 = 10.3V / 0.1mA = 103[kΩ]
R2 = 1.7V / 0.1mA = 17[kΩ]
以上で電流帰還バイアス回路を使った5倍の電圧増幅度を持つ増幅器を設計することができました。